我们应该教什么

小学和中学教师曾经向我表达他们的担心，各个年级的数学课上都有太多的知识点，没有足够的时间全部讲解。在有些情况下，重要的内容没有足够的时间讲，而一些不太重要的内容却在各个年级不断重复。就像我们都听到过的所谓“英里宽英寸厚的课程”。尽管各年级标准分布很广，每个年级仍然缺乏针对特定内容的聚焦，这种聚焦将有助于学生数学能力的逐步发展并与个人的认知发展水平相匹配。

我们在此提出的建议是由安斯沃斯和克里斯廷森（Ainsworth&Christinson，2000）提出来的。在与加州教师合作的过程中，他们赞问，从学前班到七年级，每个年级应该聚焦一个重大主题并进行深度教学。他们依据的原理是，如果学生在所在年级对某个重大主题有了深人的理解，那么在下一年级他们将不再重复学习同样的内容，而是在理解的基础上进一步学习。正如我们前面所讨论的，他们的方法与认知神经科学的观点相一致，即深入的学习产生意义，从而增加了概念被记住的可能性，并借此构筑坚实的数学能力的框架。

他们建议的适用于各个年级水平的重大主题如下：

● 学前班 数感

● 一年级 数感和加法

● 二年级 减法

● 三年级 乘法

● 四年级 除法

● 五年级 分数

● 六年级 分数、小数和百分数

● 七年级 比率和比例

当然，重大主题并非那个年级唯一讲授的概念，但它应该代表教学的主要聚焦点。八年级的内容未包含其中，因为八年级的聚焦点已被认定是代数。这看起来与NCTM数学实践与标准和许多州立数学课程框架是一致的。

教授程序性技能

理解如何操作数字、发现和分析模式、解决问题，如何将数学知识运用于真实世界，都需要掌握一定的程序性技能。NCTM的《学校数学教学原则与标准》（NCTM,2000）中包含了10个标准，其中5个是内容标准，另5个是程序标准。这些程序标准包括：（1）问题解决;（2）推理和验证;（3）沟通;（4）联系；（5）呈现。

认知神经科学研究在某种程度上揭示的与这此过程标准有关的三个内容是数感、估算（感数的副产品）和推理。

教师设计开发学生数感的课程时，重要的是要知道每个学生已经达到的数感水平。研究者莎朗·格里芬和罗比·凯斯在20世纪80年代就开始探讨这个问题。在进行了20余年的测验之后，他们根据研究结果进行了提炼，以保证题目能够反映每个年龄段大多数学生所拥有的能力（Griffin&Case,1997；Griffn,2002）。

当教师准备开发学生数感的课程时，他们应该确定每个学生已经达到的数感水平。

通过进行这些测验，教师能够确定学生从4岁、6岁、8岁到10岁时的数感发展水平，然后教师就可以对同龄但可能能力水平不同的学生采用不同的活动来发展数感。下表显示了6岁、8岁和10岁儿童适用的测验版本。

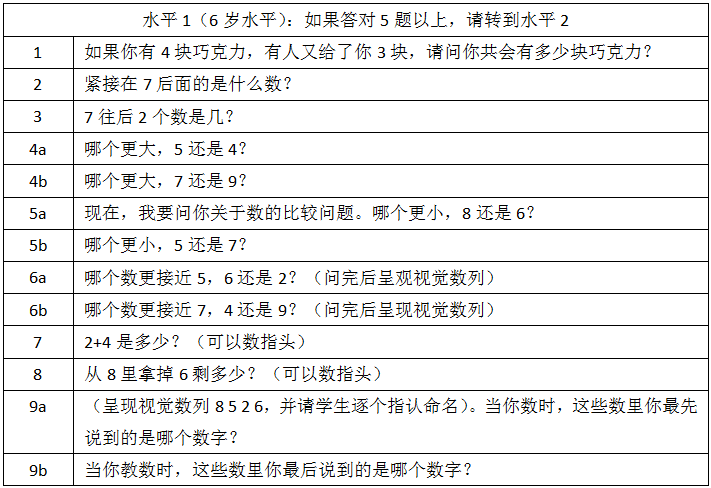
发展多位数数感

低年级学生已经发展了一定的数数概念，但在学习包含有大数字的问题时，例如一个国家的人口、星球之间的距离以及执行一个航天计划所需的费用等内容时，还是会遇到困难。尽管学生们对大数字很着迷，但对它们的理解很有限，并且他们在交谈中还常常夸大数字：“我的生日聚会来了几千人。”当学生对大数字缺乏理解时，他们无法对相应信息进行有效的分析和推理。面对这种情形教师需要发展学生对于大数字的加工能力，即，发展他们的多位数数感。

多位数数感是指学生对一位以上数字的理解和运用的灵活性，包括对于大数字的直觉和运用，以及在不同情境下对多位数的合理性进行判断（Joncs，Thormton&Ptt,1994）。由于这个问题的复杂性，教师应该选择有意义的活动帮助学生理解大数字运用的背景。

迪兹曼和英格利希（Diezmann&Engish，2001）通过选择一些活动来带助学生读大数字，建立有意义的大数字样例，理解表示数量、距离和钱数的大数字等，被证明在小学生中是有效的。

读大数字。在这个活动里，引导学生读大数字。给学生展示数量逐渐增大的数字，先从个位数开始，逐渐增大到千位数，最后到百万。同时给出数字的读法，帮助学生读取数字。

建立有关大数字的实物样例。具体的例子可以帮助学生理解不断增长的数字的特性。一个活动是用撒在分成四份的黄油面包上的彩色糖粒（装饰糖）的方式，视觉呈现表示1、10、100和1000的数量。学生在第一份面包上放上1粒糖，在第二份上放上10粒，第三份大概100粒（用10个一组的方式估计），最后一份大约1000粒（以100为一组的方式进行估计）。撒糖粒的话动为学生理解千的数量提供了有意义的例子。一些学生可能会超越实物例子进行推断，并且会发现不可能在一片面包上放上100万个小糖粒。

认识大额面值。要多大的容器才能装下100万美元？在解决这个问题之前，学生要先完成两个任务。第一个是要制作标有1、10、100、1000、10000、100000和1000000美元的标签。让学生辨认杂志和报纸广告中那些大概符合这些价钱的商品，并将标签贴在相应商品上方。这个活动帮助学生提高了对于贵重物品的金钱价值的认识。在第二个任务中，让学生计算在大富翁游戏中所花费的钱数。

在完成这些任务后，学生将努力解决盛放百万美元的容器尺寸的问题。学生应该用到大富翁游戏中的钱来帮助他们解决这个问题。鼓励学生自己动手制作不同尺寸的容器，不事先给出样例。经过讨论，学生应该意识到，正确的答案不止一个。例如，容器的尺寸取决于组成百万美元的钞票的面额。一些学生可能意识到，如果使用小面额的钞票，则需要更大的容器，反之亦然。

认识距离中的大数字。最亮的星星离我们有多远？这个活动的目的是建立学生对于宇宙范围内大的空间距离的理解。一个方法是让学生做10颗星星的模型，并用天空中最亮的10颗星星的名字给它们命名，同时标注它们的亮度和到地球的距离。星星可以贴在倒过来的纸杯上以便挪移。让学生一开始按照星星的亮度排列，从最亮的星星开始。

然后，结合星星到地球的距离进行考虑。在学生讨论了有关用光年度量星球距离的概念之后，重新按照到地球距离由近到远的顺序排列星星。通过让学生讨论在星星的亮度和到地球之间的距离有何种关系的问题进一步扩展活动。

为了展示用光年表示星星到地球的距离，画一条时间线，以100秒为间隔，从0画到1000。让学生按照到地球的光年数摆放每颗星星。然后，可以讨论他们今天看到的星星的光亮实际上是几年前发出的。年龄大一些的学生也许能将从某一特定星球上发出光亮的年代联系到在地球上发生的重大历史事件。用这种方式，学生就在他们对于数学的理解与科学知识之间建立了联系。

本文内容转载自《人脑如何学数学》一书，如存在版权问题请及时联系我们，我们坚持保护原创者的知识版权。