与数感有着密切联系的是估算。NCTM的《课程焦点》（NCTM，2006）指出，三年级学生应该能够“通过心算.....通过估算和纸笔计算的帮助，发展对于数字的理解”。在四年级，学生应该“能在不同情境下将对数字的理解和表达扩展到100000，他们在判断数量或距离的相对大小时会运用估算”。

估算是大脑感数天赋的一种延伸。估算要捕猎多少头动物，或者需要种多少粮食才够全村人吃的能力是一种生存技能。我们的祖先善长此道。数学教育者常常批评学生薄弱的估算能力。有一次，一个沮丧的老师告诉我，一个中学生在算出一个分子有一米长之后还感到非常高兴。他从来没有见过这么不合理的测量结果。然而，具有讽刺意味的是，年轻人在学校之外却常常能够成功运用估算技能。例如，他们能够很快地估算穿过拥挤的马路需要多长时间，判断兄弟间是否平均分配，或者精准地计算在比赛中投球、截球和击球。那些较差的估算状况似乎仅出现在学校里，当面对计算上的估算问题时才表现出来。而这可能至少有三个原因。

第一，学生在较小的时候被教导要获得问题的准确答案，他们没有多少关于估算的经验。另外，那些让学生同时给出估算和精算答案的活动降低了估算的意义。既然要学生去获得准确答案，他们为什么还要去估算呢?

第二，当学生在作业中使用计算器时，他们就会认为计算器给出的答案一定是正确的，他们就不去想会不会不小心输错了数字或输错了小数点的位置。于是，他们几乎不会去反思答案的合理性。

第三，由于学生想要尽快获得答案，于是往往会避免使用占用更多时间的估算。

涉及估算的活动应该在低年级尽早开展。然而它们不应该被孤立为一个单独的教学单元，而应该贯穿于所有年级水平的其他数学技能的教学中。如果我们想要强调估算的意义，那么就应该给学生布置只需要估算的任务。

估算的方法

通常估算的方法有几种:（1）凑整，是指找出最接近数字的整十、整百、整千的数或最接近的个数、十分之一、百分之一、千分之一的数；（2）首尾估算，这是指从最高的或最左边数位开始算，然后根据低位或右边数值对总数进行调整；（3）聚类，这涉及将数字分组，这个方法只要在一组数都接近某一共同值时就会有用。这些估算方法在学生完成计算任务时极其有用，他们能够检查获得的答案是否接近估算的答案并判断答案是否合理。

学生需要认识到，估算的方法在实际生活中可能并不适用。如果你想买件17.45元的衬衫，往下凑整到最接近的整数价钱并不能让你有足够的钱买下这件衬衫。在涉及有关测量的估算也是如此，如果你需要准确的三又四分之一码的布来做一件衣服，你估算成只要三码就没法做成。因此，在现实生活情境中，向下凑整的估算方法对你来说是不够的。还有什么其他的估算方法么?

估算的类型

泰勒科克斯（Taylor-Cox，2001）提出了四种不同的估算类型。

（1）真实估算往往用于当一个估算的数可以被接受时，特别是对于非常大的数。知道从地球到太阳的平均距离到底是92955630英里还是93000000英里真的很重要吗?真实估算通常适用于中年级或更高年级的问题。但遗憾的是，低年级的学生所遇到的数字通常较小而且比较简单，往往不适于使用真实估算。真实估算对于那些简单的数而言没有优势，因为我们能够很容易算出准确数值。

（2）高估通常用于向上凑整可能对我们有利时，比如估算孩子生日聚会所需的食品。这种方法的主要缺点是当你高估太多时可能导致浪费，但是如果你低估了，一些孩子就可能无法获得足够的食物。

（3）低估通常用于向下凑整的时候，这在某些特定情境下会有用。例如最好低估商业所得利润以避免过度支出。

（4）范围限定的估算将扩展对估算的理解及其适用性。一些情境要求低估而一些要求高估。一定范围内的估算是指在遇到一个估算问题时思考所涉及数量的高限和低限。“我最少需要多少，最多又需要多少?”在小学，教师可以用一定范围内估算的方法设计有创造性和有意义的数学任务，从而促进学生成为更好的估算者。

有意义的估算活动

为了使估算行为成为有意义的活动，泰勒科克斯（Taylor-Cox，2001）提出的相关活动包括以下五个部分。

目的。当你要求学生估算一个数值时，都要给他们需要估算的理由。这个内容为学生解决与实际生活相关的数学问题提供了目的和理由。否则，学生会问:“谁会需要这个?”让任务变得有关联性、有趣和重要，会让学生关注数学，从而让他们能够投入到数学活动中。提供目的并不能保证诸如“谁会需要”这样的问题消失。但是通过听取学生的意见并对他们的观点和感觉进行回应，你就能够应对不断遇到的要求为数学提供意义的难题。

参照物（基准）。为了帮助学生成功，可以在他们进行估算时提供一个可以使用的参照物或基准。例如，当你要求学生估算一个瓦罐里的弹珠数目时，给他们提供一个在较小的容器里能够盛放的弹珠数目可能会帮他们完成任务。这个容器就为学生提供了个参照，从而使他们可以在此基础上估算较大罐里盛放的弹珠数目。

相关信息。澄清所需解决的实际数学问题能够帮助学生确定哪种估算方法最合适。例如，如果学生要打开瓦罐并且数出弹珠的准确数量他们就不需要估计弹珠的数目。正如之前解释的，这样做是与估算的目的相冲突并浪费时间的。相反地，你需要问问自己估算和准确计数哪个更合适。会用哪种方法来核查准确性?什么样的信息与给定的数学情景有关?

多样性经验。学生需要获得在其他领域中大量且多样的估算经验，例如时间和测量。小学生在估算时间时通常会感到困难，教师在表述时使用不准确的时间限定对此没有帮助。当他们说“我会在一分钟之内到那里”或者“等一秒钟”时，实际意味着“我会尽快赶到那里”或“等着吧”。或许让学生给老师计时能够促使他们反思对时间的估算，从而增强他们的经验并提高他们估算时间的精确性。

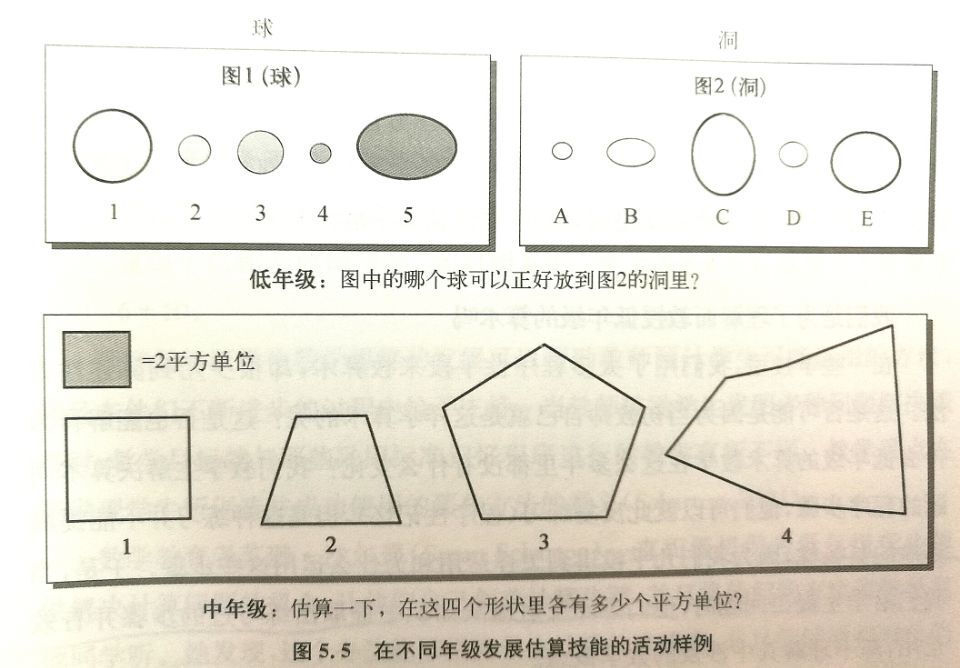
年纪小的学生通过比较长度、重量和容量来练习测量技能。为了估算大小，他们需要用到比较的语言表达，比如说，更大、更小、更重和更轻。图5.5显示了两个不同年级组需要估算大小的活动案例。在这几种任务中，学生进行的估算更多地与物体的大小有关而不是与数量有关，他们认识到估算是处理日常测量问题的重要工具。

范围限定技术。估算应该在合理范围内运用数学技能进行预测。比如说，一个量或一个测量的准确数值是70多，那么合适的估算就应该在10个估算误差值以内或者更少。但如果准确数值是700多，那么合适的估算误差范围可能就扩展到60~70个数。虽然问题情境不同，合适的范围也不同，但这样做的目的是为了让估算能够在合适的范围内进行。然而，许多学生仍然想要估算出精确的量。为了与这种寻求正确答案的需求抗争，使用实际答案之类的术语或许能奏效。每100数值的估算误差范围在10或20之内都是合理的。在碰到需要估算而又很可能高估的情况时，这种范围限定的估算尤其有用。

估算的体验可以提高学生的估算技能，增强他们对于自己数学专业知识掌握程度的自信，加强他们对于数学意义的感知并提高他们数学成就测验的分数（Booth&Siegler.2006）。每个估算活动对于教师而言，都是次很好的将数学与学生的日常生活建立联系的机会。

本文内容转载自《人脑如何学数学》一书，如存在版权问题请及时联系我们，我们坚持保护原创者的知识版权。